関数の型の代入可能性

関数の型もやはり、さまざまな関数を要素とする集合です。

例えば

function add(a: number, b: number): number {
    return a + b
}

function sub(a: number, b: number): number {
    return a - b
}

の２つの関数は同じ(a: number, b: number) => numberという型に属する関数です。

しかし、関数の型に関数が代入可能であるかどうかを判定する際、その集合の要素であるかどうかというルールには従いません。少し特別なルールに従うこととなります。その結果、その型の部分型が代入できなかったり、さらにはその型の要素ですらないようなものが代入できたりします。

// 部分型が代入できない例
const a: (n: number) => number = (n: 1 | 2) => { // ERROR!
    return n
}

// 型の要素でないものが代入できる例
const b: (n: number) => number = (n: number | string) => { // OK!
    return n
}

これはなぜでしょうか？理論的な説明は難しいかもしれませんが、理由は簡単です。上はエラーになる可能性があって、下は（基本的に）ならないからです。

少し極端な例を見てみましょう。

TypeScriptには全ての値の集合であるunknown型が存在します。そうすると、全ての一引数関数というのは(a: unknown) => unknown型に所属する要素であると言えます。

そしてこれまで通りのルールで部分型が代入可能であるとするのであれば、unknown => unknown型にはnumber => number型が代入可能ということになります。

具体的に言えば以下のようなことがOKということです（実際にはダメですので気をつけて ）。

const a: (n: unknown) => unknown = (n: number) => {
  return 2 * n
}

ふむふむ。ではこの関数を実際に呼び出してみましょう。引数の型はunknownなのでどのような型の値であってもOKですね。文字列"hello"をわたしてみましょうか。

a("hello")

本当に良いのでしょうか...?確か関数の実装の中では引数がnumber型である前提のもと、引数に２を掛けていたずです。

もちろんだめです。もしこれをTypeScriptが許したとしても実行時エラーが発生します。

このように、これまでの「代入可能性」の定義ではエラーを回避するのに不十分になってしまいます。そこで関数に対しては別のルール（より抽象的にみた場合にはどちらも同じ定義なのかもしれません）が存在します。

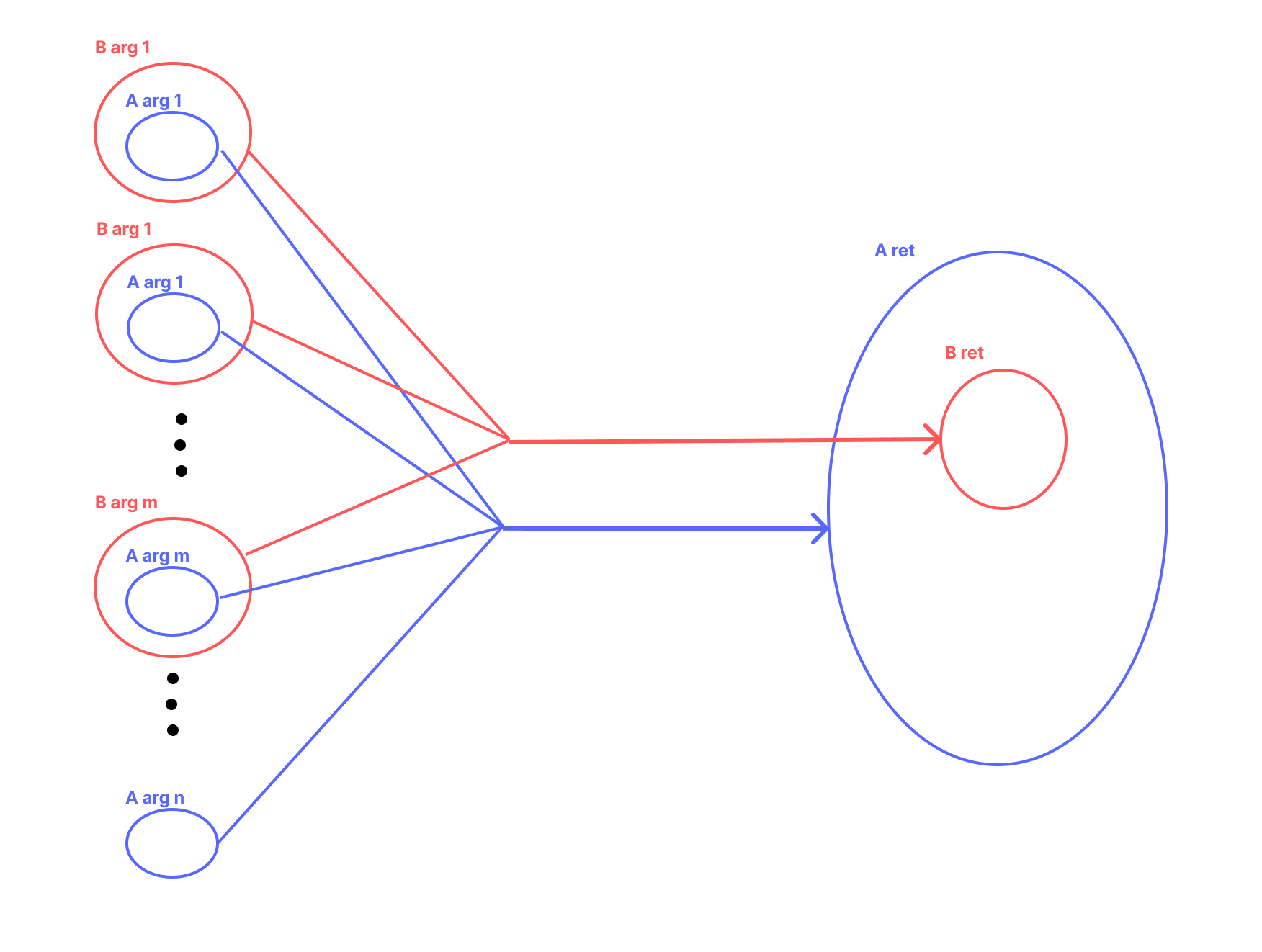
定義は以下のとおりです。

二つの関数の型

• $A = (A_{arg\ 1}, A_{arg\ 2}, ..., A_{arg\ n}) => A_{ret} (n \geqq 0)$
  • nが0というのは引数の個数が0個ということ
• $B = (B_{arg\ 1}, B_{arg\ 2}, ..., A_{arg\ m}) => B_{ret} (m \geqq 0)$
  • mが0というのは引数の個数が0個ということ

があって、

1. $n \geqq m$
2. $\forall i \in \mathbb{N}(1 \leqq i \leqq m), A_{arg\ i} \subset B_{arg\ i}$
3. $B_{ret} \subset A_{ret}$

のとき、型Aに型Bを代入可能となります。

日本語でおkすると、

1. Aの引数よりBの引数の方が個数が少ない
2. 全てのBの引数の型と対応するAの引数の型について、後者が前者の部分型である
3. Bの返り値の型がAの返り値の型の部分型である

図にすると以下のような感じです。

また集合の直積を知っている場合には以下ようにしてもよい(と思います)。

1. $n \geqq m$
2. $\displaystyle \prod_{i = 1}^m A_{arg\ i} \subset \prod_{i = 1}^m B_{arg\ i}$
3. $B_{ret} \subset A_{ret}$

こうすると若干図がシンプルにできて、

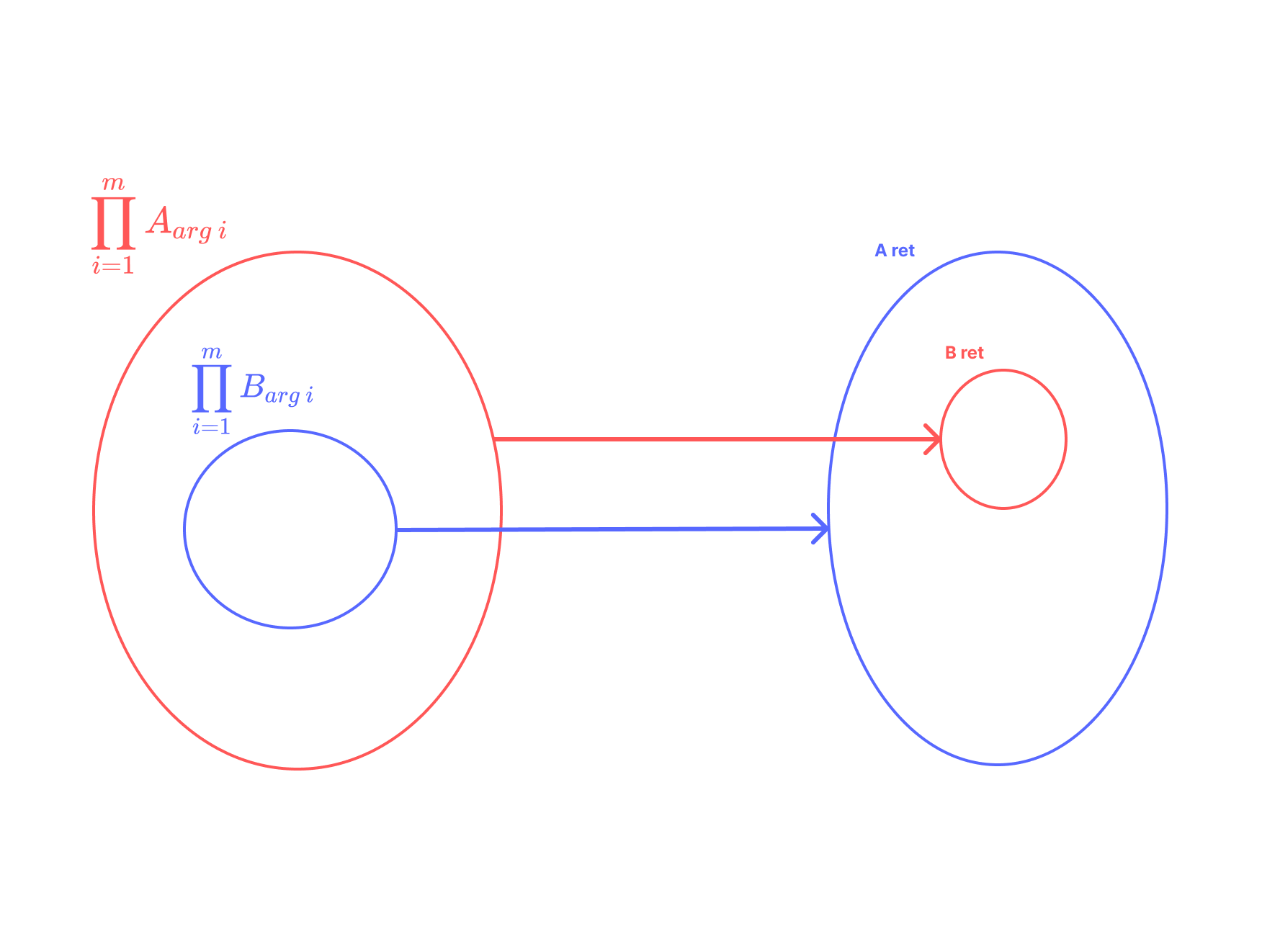
となります。(あってるよね？)